For the SPX Friday 28 June 2024 meets the criteria for a peak (bearish) Key Reversal Day:
‘Key Reversal Day: In a bearish key reversal the market OPENS above the prior close, often leaving a gap, sets a new high, and then closes the day lower than the prior day’s close.’

A two day chart from 27 and 28 June 2024 is shown for the SPX below.

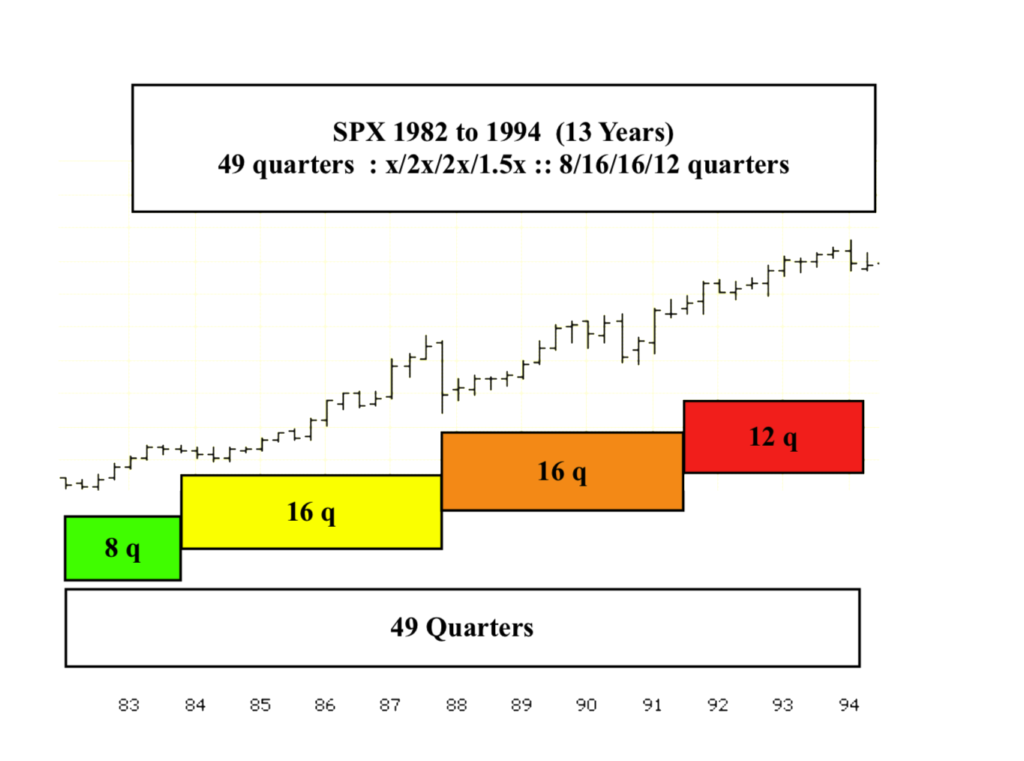
28 June 2024 for the SPX represents year 31 of a 13/31-33 year 1982 first and second fractal series. As an update from the second picture below 28 June represents the 121 quarter of a 49-50/123-125 quarter first and second fractal series

For the SPX 28 June 2024 represents day 114 of a 55/112-140 day 27 October 2023 first and second fractal series. The SPX is in the terminal 2x to 2.5x portion of the 112-140 second fractal window where nonlinear occurs.

US total market cap to GDP ratio was at 193.3 % on 27 June 2024, still more than 6% below its 2021 199.5% peak.

Second Fractal Nonlinearity:

From the 2005 website page of TEF regarding first and second fractals (cycles) of a 4 phase fractal (cycle) (x/2x-2.5x/2x(to 2.5x)/1.5-1.6x series.

…. “The first two cycles include a saturation transitional point and decay process in the terminal portion of the cycles. A sudden nonlinear drop in the last 0.5x time period of the 2.5X is the hallmark of a second cycle (fractal)and characterizes this most recognizable (fractal) cycle.”

Second Fractal Nonlinearity

Why did significant one day crashes occur on 19 Oct 1987 and on 6 May 2010? What news precipitated these events? The explanation of Fractal Macroeconomics is that both occurred in the terminal 2x to 2.5x window of second fractals, when nonlinear price devaluations can occur in saturated oversold markets. 1929 to 1932 occurred at the end of a US hegemonic 90 year second fractal occurring as a 36/90 year series starting in 1807.

Currently, this is year 31 of a 13/31-33 year 1982 first and second fractal series and day 113-114 (for the SPX and DAX respectively) of a 56/112-140 day October 2023 first and second fractal series. The system is in the terminal 2x to 2.5x second fractal windows. For the Wilshire 25 June 2024 did not exceed its 18 June 2024 nominal peak but did serve as a secondary near peak valuation of a 8/24/22 month fractal growth series from the March 2020 low.

The asset debt system is in the 2x to 2.5x time window of both the 1982 and Oct 2023 second fractal nonlinearity.

Will there be an incipient (and AI propelled) flash crash?

US total market cap to GDP ratio was at 192.2 % on 24 June 2024, still 7% below its 2021 199.5% peak.

Since 2020 profoundly and historically aberrationally high deficit borrowing and spending (as a % of GDP) by central banks, governmental, and private sources – has produced relatively so little GDP.

Expect the unexpected.

Copper, the global useful building element commodity is following the same March 2020 monthly fractal pathway as the German Dax : 8-9/24/22 months. The 24 month second fractal is composed of a 4/9/8/6 exactly paralleling the German Dax.

The weekly German Dax from the low in October 2023 is composed of two fractal series: an initial 3/6/6 of 13 week first fractal series and a 5/10/10/1 of 7 week or 29 week second fractal series. This should end in about the last wee of July 2024.

With weakening economic data, the European and Canadian central banks have already lowered sovereign interest rates. A significant July 2024 drop in global equities will likely precipitate another round of central bank interest rate cuts and an initial Federal Reserve Fed Funds rate cut. A third fractal rebound of about 23-24 weeks would take equity growth beyond the United States early November 2024 presidential election.